امتحان نهائي الرياضيات الصف الثاني عشر عام الفصل الثالث الامارات
ملفات اخرى
-
كتاب
 كتاب الاحياء الصف الثاني عشر عام الفصل الثالث pdf 2025
كتاب الاحياء الصف الثاني عشر عام الفصل الثالث pdf 2025 -
اوراق
 اوراق عمل احياء الثاني عشر عام الفصل الثالث الامارات
اوراق عمل احياء الثاني عشر عام الفصل الثالث الامارات -
مراجعة
 مراجعه شاملة الاحياء الثاني عشر عام الفصل الثالث الامارات
مراجعه شاملة الاحياء الثاني عشر عام الفصل الثالث الامارات -
اختبار
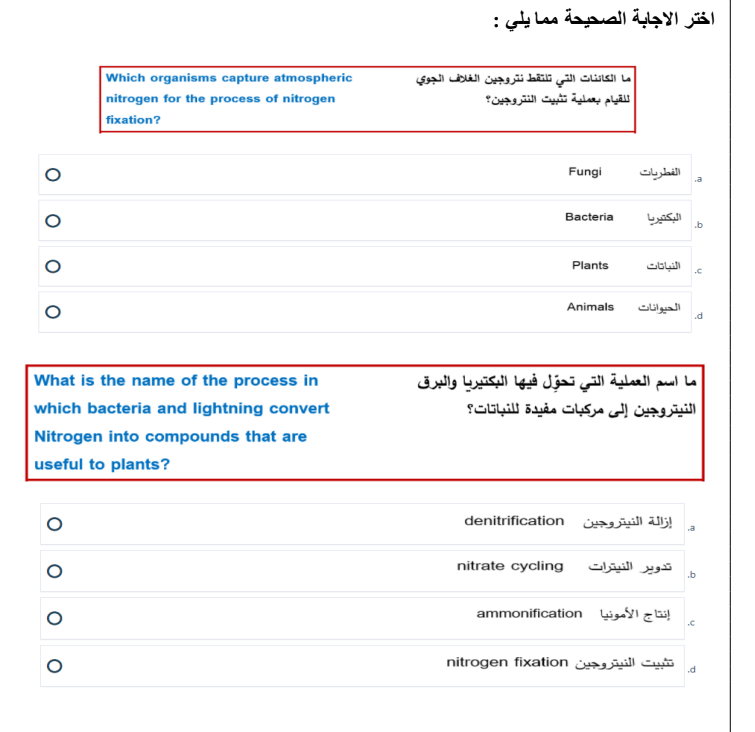 امتحان نهائي احياء الصف الثاني عشر عام الفصل الثالث الامارات
امتحان نهائي احياء الصف الثاني عشر عام الفصل الثالث الامارات -
كتاب
 كتاب الطالب تطبيقات نحوية الثاني عشر الفصل الثالث pdf
كتاب الطالب تطبيقات نحوية الثاني عشر الفصل الثالث pdf -
كتاب
 كتاب التطبيقات اللغوية الثاني عشر الفصل الثالث 2025 pdf
كتاب التطبيقات اللغوية الثاني عشر الفصل الثالث 2025 pdf
اختبار نهائي رياضيات الصف الثاني عشر عام الفصل الدراسي الثالث المنهج الاماراتي للعام الدراسي الجديد , امتحان نهائي الرياضيات ثاني عشر عام الفصل الثالث pdf.
إجابة اختبار نهائي رياضيات الصف الثاني عشر عام الفصل الثالث
ما مدى الدالة y = 2x^(-2) - 1؟
الخيارات:
a) (-∞, -1]
b) (-1, ∞)
c) (0, ∞)
d) (-∞, ∞)
السؤال 2
إذا كانت الدالة كثيرة الحدود f من الدرجة n >= 1، ما أكبر عدد ممكن من نقاط الدوران لهذه الدالة؟
الخيارات:
a) n
b) n - 1
c) n + 1
d) n - 2
السؤال 3
أي دالة كثيرة حدود من الدرجة n = 4 و لها صفران حقيقيان فقط؟
الخيارات:
a) f(x) = x^3 - x^2
b) f(x) = x^4 - x^3
c) f(x) = x^4 - 8x^2 + 15
d) f(x) = x^4 + 3x^2 - 4
السؤال 4
ما هو السلوك الطرقي للرسم البياني للدالة f(x) = -2x^3 + 3x^2 + x - 3؟
الخيارات:
a) lim x→∞ f(x) = ∞ و lim x→-∞ f(x) = -∞
b) lim x→∞ f(x) = ∞ و lim x→-∞ f(x) = ∞
c) lim x→∞ f(x) = -∞ و lim x→-∞ f(x) = ∞
d) lim x→∞ f(x) = ∞ و lim x→-∞ f(x) = -∞
الأسئلة
السؤال 1
وفقاً لقاعدة ديكارت للاشارات، كم عدد الأصفار الحقيقية السالبة التي يمكن أن تحتوي عليها الدالة؟
الخيارات:
a) 0 أو 2
b) 1
c) 3 أو 1
d) لا يوجد أصفار سالبة
السؤال 2
ما قيمة k بحيث يكون (x - 1) عاملاً لكثيرة الحدود x^3 + 4x^2 - kx + 1؟
الخيارات:
a) k = -1
b) k = 1
c) k = 4
d) k = -4
السؤال 3
أي من العبارات التالية يمكن استخدامها لوصف السلوك الطرفي للدالة f(x) = 6x^5 - 8x^2 - 10x - 15؟
الخيارات:
a) lim x→-∞ f(x) = -∞ و lim x→∞ f(x) = -∞
b) lim x→∞ f(x) = -∞ و lim x→-∞ f(x) = ∞
c) lim x→-∞ f(x) = -∞ و lim x→∞ f(x) = ∞
d) lim x→-∞ f(x) = ∞ و lim x→∞ f(x) = ∞
السؤال 4
أي من العبارات التالية تمثل دالة؟
الخيارات:
a) |x - 4|
b) |x - 3|
c) |x|
d) |3x|
أوجد قيمة log₃(∛[5]27)
a) -5
b) 3/5
c) 9
d) -3/5
عبر عن ln(36/25) باستخدام ln(6) و ln(5)
a) ln(6) - ln(5)
b) ln(6) - 2 * ln(5)
c) 2 * ln(6) - ln(5)
d) 2(ln(6) - ln(5))
حدد الدالة التي يوضحها التمثيل البياني المجاور
a) y = 50 - x
b) y = e^(-x)
c) y = log(x)
d) y = 2^x
حدد تقاطع الدالة y = log(x + 7) مع محور x
a) x = 7
b) x = -7
c) x = -6
d) x = 6
حدد الدورة للدالة y = 3cos(x/2) - 1
a) π
b) 3π
c) 4π
d) 2π
أوجد طول القوس المحصور بقياس الزاوية المركزية θ = 30° في دائرة نصف قطرها r = 6cm
a) π
b) 2π
c) π/2
d) 4π
أوجد مساحة قطاع الدائرة إذا كان قياس زاويته المركزية θ = (2π)/3 و نصف القطر r = 3cm
a) 2π
b) 3π
c) π
d) 4π
إذا كان cos(x) = 0.81، فأوجد sin(x - π/2)
a) 0.81
b) -0.81
c) -0.19
d) 0.19
أوجد مساحة المثلث ΔABC الذي فيه a = ?, c = 4cm, b = 6cm, A = 120°
(الخيارات تحتاج إلى توضيح القيمة a)
a) 6√3
b) 12
c) 6
d) 12√3